File operations can throw exceptions because not find file, hit end of file when reading, etc.! In Java, one must test for exceptions and provide code to execute when exceptions are raised.
Java file operations may raise exceptions of type IOException. Must surround code that may throw this exception by:
try {
//code using files
} catch (IOException exc) {
//code to execute if exception raised
}
In the above, exc is a parameter of type IOException. You can send it a toString message to get info on what went wrong in the block that follows it.
You can either put all of the code into one single try-catch block or put each command that may raise the exception in such a block. You will get syntax errors if you do not surround these file messages with a try-catch block.
Your program should not just ignore these exceptions. At a minimum it should print out a message and return to a consistent state.
public void doInorder()
{
reset(); // move cursor to root
if (root != null) doRecInorder();
}
/*
post: Do inorder traversal of subtree pointed to by
cursor. Return cursor to starting point when done.
*/
public void doRecInorder()
{
if (hasLeft())
{
moveLeft();
doRecInorder();
moveUp();
}
value().doValueOp();
if (hasRight())
{
moveRight();
doRecInorder();
moveUp();
}
}
It's very important to move the cursor back to where you started, otherwise the recursive solution will not work.

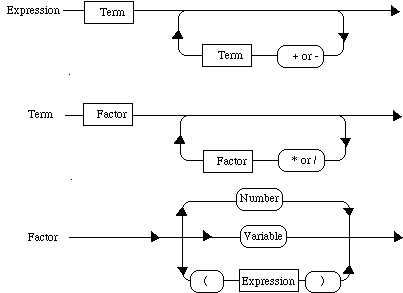
What do we know about first possible characters of Factor, Term, or Expression?
Can use to help catch errors.
Look at how 3 * 7 + 6 / 2 - (3 + 7) would be understood as a tree.
3*7 is a term because both 3 and 7 are factors, similarly 6/2 is a term.
(3+7) is a factor because 3 + 7 is is an expression.
Because it is a factor, it is also a term.
Therefore 3 * 7 + 6 / 2 - (3 + 7) is of the form term1 + term2 - term3, and hence is an expression!
Exercise: Write out the corresponding tree (remember operations of the same precedence are done from left to right.)
Once you have the tree, how do you evaluate it?
See Parser code on-line.
Two things to notice:
The array, data[0..n-1], holds the values to be stored in the tree. It does not contain references to the left or right subtrees.
Instead the children of node i are stored in positions 2*i +1 and 2*i + 2, and therefore the parent of a node j, may be found at (j-1)/2
The following example shows how a binary tree would be stored. The notation under the tree is a "parenthesis" notation for a tree. A tree is represented as (Root Left Right) where Root is the value of the root of the tree and Left and Right are the representations of the left and right subtrees (in the same notation). Leaves are represented by just writing their value. When a node has only one subtree, the space for the other is filled with () to represent the absence of a subtree.
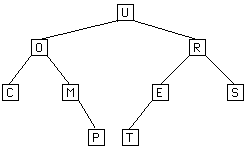
Ex. (U (O C (M () P) ) (R (E T () ) S) )
IndexRange: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
data[]: U O R C M E S - - - P T - - -
Save space for links, but it is possible that there is exponentially much wasted storage:
Storing a tree of height n requires an array of length 2sup4(n) - 1 (!), even if the tree only has O(n) elements. This makes this representation very expensive if you have a long, skinny tree. However it is very efficient for holding full or complete trees.
Def: A Min-Heap H is a complete binary tree such that
1) H is empty or
2a) The root value is the smallest value in H and
2b) The left and right subtrees of H are also heaps.
This is equivalent to saying that H[i] <= H[2*i+1], H[2*i+2] for all approp values of i in the array representation of trees. Another way of looking at Min-Heap is that any path from a leaf to the root is in non-ascending order.
This turns out to be exactly what is needed to implement a priority queue.
A priority queue is a queue in which the elements with lowest priority values are removed before elements with higher priority.
public interface PriorityQueue {
public Comparable peek();
// pre: !isEmpty()
// post: returns the minimum value in priority queue
public Comparable remove();
// pre: !isEmpty()
// post: returns and removes minimum value from queue
public void add(Comparable value);
// pre: value is non-null comparable
// post: value is added to priority queue
public boolean isEmpty();
// post: returns true iff no elements are in queue
public int size();
// post: returns number of elements within queue
public void clear();
// post: removes all elements from queue
}
One can implement a priority queue as a regular queue where either you work harder to insert or to remove an element (i.e. store in priority order, or search each time to remove lowest priority elements).
Unfortunately, in these cases either adding or deleting an element will be O(n). (Which one is O(n) depends on which of the two schemes is adopted!)
Can provide more efficient implementation with heap!
- remove element with lowest priority (at root of tree) and then remake heap.