CS334 Lecture 4

CS334 Lecture 4 Lazy Evaluation

9. Lazy vs. Eager evaluation

At some cost in execution efficiency, can add extra power to language by supporting lazy evaluation - also called call-by-need or normal order evaluation.

Order of operations: Eager: Evaluate operand, substitute operand value in for formal parameter, and evaluate.

Lazy: Substitute operand in for formal parameter and evaluate, evaluating operand only when needed. Notice each actual parameter evaluated either not at all or only once!

Ex.

- fun test (x:{a:int,b:unit}) = 
    		if (#a{a=2,b=output(std_out,"A")} = 2) 
			then (#a x) 
			else (#a x);
> val test = fn : { a:int, b:unit } -> int
- test {a = 7, b = output(std_out,"B")};

If have eager evaluation, get:

BA
> 7 : int

If have lazy evaluation, get:

AB
> 7 : int

Notice that call-by-need is equivalent to call-by-name in functional languages, but can be implemented more efficiently since when evaluate argument, can save value (since it won't change).

Can also share different instances of parameter.

E.g.,

	fun multiple x = if x = [1,2,3] then 0::x else x@[4,5,6]

When substitute in value for x, don't really need to make three copies (again, since can't change!)

Lazy evaluation allows programmer to create infinite lists.

Ex. (in lazy dialect of ML)

fun from n = n :: from (n+1)
val nats = from 1;
fun nth 1 (fst::rest) = fst
  | nth n (fst::rest) = nth (n-1) rest

Can get approximate square root of x by starting with an approximation a0 for sqrt and then getting successive approximations by calculating

		an+1 = 1/2 * (an + x/an)

Program infinite list of approximations by:

fun approxsqrts x =
	let from approx = approx :: from (0.5 * (approx + x/approx))
	in from 1.0
	end;

If want approximation where difference between successive approximation is < eps,

fun within eps (approx1 :: approx2 :: rest) =
	if abs(approx1 - approx2) < eps 
			then approx1
			else absolute eps (approx2::rest);

Now to get sqrt approx in which diff btn successive terms is < eps then write:

fun sqrtapprox x eps = within eps (approxsqrts x)

Of course can also do with eager language, but bit more to worry about - must combine logic of both approxsqrts and within into same function.

Why not just use lazy evaluation?

Eager language easier and more efficient to implement w/ conventional techniques.

If language has side-effects, then important to know when they will occur!

Also many-optimizations involve introducing side-effects into storage to save time.

In parallelizing computation, often better to start computation as soon as ready. With eager evaluation, know evaluation of parameter won't be wasted.

Can simulate lazy evaluation in eager language by making expressions into "parameterless" functions.

I.e., if wish to delay evaluation of E : T, change to fn : () => E of type unit -> T.

Ex: Spose wish to implement second parameter of f with lazy evaluation:

   f x y = if x = [] then [] else x @ y

Rewrite as

  f' x y' = if x = [] then [] else x @ (y' ())  (* note y' applied to element of type unit *)

If would normally write:
f E1 E2, instead write f' E1 (fn () => E2)

Then E2 only evaluated if x != []!

Implement lazy lists, Suspended lists, in an eager language:

   datatype 'a susplist = Mksl of (unit -> 'a * 'a susplist) | Endsl;

Like regular list, but must apply to () before get components!

(* add new elt to beginning of suspended list *)
fun slCons newhd slist = let fun f () = (newhd, slist)   
                    	 in Mksl f end;

exception empty_list;

(* extract head of suspended list *)
fun slHd Endsl = raise empty_list
  | slHd (Mksl f) = let val (a,s) = f ()
                    in a end;

(* extract tail of suspended list *)
fun slTl Endsl = raise empty_list
  | slTl (Mksl f) = let val (a,s) = f()
                    in s end;

(* Is suspended list empty? *)
fun slNull Endsl = true
  | slNull(Mksl f) = false;
  
(* Infinite list of ones as suspended list *)
val ones = let fun f() = (1,Mksl f)
           in Mksl f end;
           
(* Suspended list of increasing integers starting with n *)
fun from n = let fun f() = (n, from(n+1))
             in Mksl f end;
             
val nat = from 1;

Languages like LISP and SCHEME as well as lazy languages support streams for I/O.

10. Higher-order functions

Fcnal languages provide new kind of "glue" allowing programmer to write small modules and "glue" them together into larger programs. (See Hughes article)

Can build own glue by writing higher order functions.

Can write product on lists by writing

fun prod [] = 1
  | prod (head::rest) = head * prod rest

Similarly for

fun sum [] = 0
  | sum (head::rest) = head + sum rest

Notice general pattern and write higher-order "listify" function:

fun listify oper (identity:'a) ([]:'a list) = identity
  | listify oper identity (fst::rest) = 
                        oper(fst,listify oper identity rest);
> val listify = fn : (('a * 'a) -> 'a) -> ('a -> (('a list) -> 'a))

then

val listsum = let fun sum(x,y) = x+y:int 
              in listify sum 0 
              end;
val listmult = let fun mult(x,y) = x*y:int 
                in listify mult 1 
                end;
val length = let fun add1(x,y) = 1 + y 
             in listify add1 0 
             end;
fun append a b = let fun cons(x,y) = (x::y) 
                 in listify cons b a 
                 end;

Can define other higher-order functions as glue also.

Can also string together programs as pipeline generating, filtering and transforming data.

(Works best with lazy evaluation)

Look back at Sqrt function w/ lazy lists.

	fun sqrtapprox x eps = within eps (approxsqrts x)

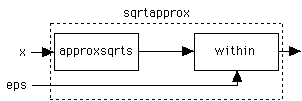
Think of program as composition of boxes, glued together by pipes (like UNIX pipes).

Lazy evaluation gives proper behavior so don't stack up lots of data between boxes.

Last box requests data from earlier boxes, etc.

In general try to write general boxes which generate, transform and filter data.

11. Program Correctness

Referential transparency is key to ease of program verification, because we can replace identifiers by their values.

I.e. If have

   let val I = E in E' end;

then get same value by evaluating E'[E/I], i.e., replace all occurrences of I by E in E' and then evaluate .

Thus we can reason that:

let val x = 2 in x + x end
    = 2 + 2
    = 4

If side effects are allowed then this reasoning fails:

Suppose print(n) has value n and induces a side-effect of printing n on the screen. Then

let val x = print(2) in x + x end
     != print(2) + print(2)

Interestingly, our proof rule only works for lazy evaluation:

let val x = m div n in 3 end;
     = 3  only if n != 0!

In lazy evaluation this is always true.

Therefore can use proof rule only if guarantee no side effects in computation and all parameters and expressions converge (or use lazy evaluation).

General theorem: Let E be a functional expression (with no side effects). If E converges to a value under eager evaluation then E converges to the same value with lazy evaluation (but not vice-versa!!)

Let's see how you can give a proof of correctness of a functional program:

fun fastfib n : int = let 
                         fun fibLoop a b 0 = a
                           | fibLoop a b n : int = fibLoop  b (a+b) (n-1)
                       in fibLoop 1 1 n
                       end;

Prove fastfib n = fib n where

fun fib 0 = 1
 |  fib 1 = 1
 |  fib n = fib (n-2) + fib (n-1);

Let ai = fib i, for all i.

Therefore a0 = a1 = 1, and ai + ai+1 = ai+2 for all i >= 0, by def of fib.

Theorem: For all i, fibLoop ai ai+1 n = ai+n.

Pf by induction on n:

If n = 0, fibLoop ai ai+1 0 = ai = ai+0 by def.

Suppose true for n - 1: Then

fibLoop ai ai+1 n = fibLoop ai+1 (ai + ai+1) (n - 1) 
                  = fibLoop ai+1 ai+2 (n - 1) 
                  = ai+1+(n-1)
                  = ai+n.

Now fastfib n = fibLoop 1 1 n = fibLoop a0 a1 n = a0+n = an by the Theorem.

Therefore, for all n, fastfib n = fib n.

Similar proofs can be given for other facts, e.g.,

   nlength (append l1 l2) = nlength(l1) + nlength(l2)

where

fun nlength [] = 0
  | nlength (h::rest) = 1 + nlength rest

and

fun append [] l2 = l2
  | append (h::rest) l2 = h :: (append rest l2)

12. Imperative features - references

Ref is a built-in constructor that creates references (i.e. addresses)

Example

- val p = ref 17
> val p = ref 17 : int ref

Can get at value of reference by writing !p

- !p + 3;
> val 20 : int

Also have assignment operator ":="

- p := !p + 1;
> () : unit
- !p;
> val 18 : int

Other imperative commands:

(E1; E2; ...; En) - evaluate all expressions (for their side-effects), returning value of En

while E1 do E2 - evaluates E2 repeatedly until E1 is false (has type unit)

Writing Pascal programs in ML:

fun decrement(counter : int ref) = counter := !counter - 1;
fun fact(n) = let val counter := ref n
                  and total = ref 1
              in while !counter > 1 do
                     (total := !total * !counter ;
                      decrement counter);
                 !total
               end;

There are restrictions on the types of references - e.g., can't have references to polymorphic objects (e.g., nil or polymorphic fcns).

7. Implementation issues

Efficiency:

Functional languages have tended not to run as fast as imperative: Why?

Use lists instead of arrays - linear time rather than constant to access elements.

Passing around fcns can be expensive, local vbles must be retained for later execution. Therefore must allocate from heap rather than stack.

Recursion typically uses lot more space than iterative algorithms. New compilers detect "tail recursion" and transform to iteration.

Lack of destructive updating. If structure is changed, may have to make an entirely new copy (though minimize through sharing). Results in generating lot of garbage so need garbage collection to go on in background.

"Listful style" - easy to write inefficient programs that pass lists around when single element would be sufficient (though optimization may reduce). If lazy evaluation need to check whether parameter has been evaluated - can be quite expensive to support. Need efficient method to do call by name - carry around instructions on how to evaluate parameter - don't evaluate until necessary.

Program run with current implementation of Standard ML of New Jersey is estimated to run only 2 to 5 times slower than equivalent C program. (Uses continuations.)

Lazy would be slower.

What would happen if we designed an alternative architecture based on functional programming languages?

Concurrency

One of driving forces behind development of functional languages.

Because values cannot be updated, result not dependent on order of evaluation.

Therefore don't need explicit synchronization constructs.

If in distributed environment can make copies w/ no danger of copies becoming inconsistent.

If evaluate f(g(x),h(x)) can evaluate g(x) and h(x) simultaneously (w/ eager evaluation).

In CSCI 135 talk about data-driven and demand-driven parallel architectures.

Demand driven (like reduction machine) support lazy evaluation.
Data driven (like dataflow architectures) support eager evaluation.

Elts of these are being integrated into parallel computer designs.

Idea is programmer need not put parallel constructs into program and same program will run on single processor and multi-processor architectures.

Not quite there yet. Current efforts require hints from programmer to allocate parts of computation to different processors.

Summary

Functional programming requires alternative way of looking at algorithms.
Referential transparency supports reasoning about programs and execution on highly parallel architectures.
While lose assignment and control/sequencing commands, gain power to write own higher-order control structures (like listify, while, etc.)
Some cost in efficiency, but gains in programmer productivity since fewer details to worry about (higher-level language) and easier to reason about.
Languages like ML, Miranda, Haskell, Hope, etc. support implicit polymorphism resulting in greater reuse of code.

ML features not discussed:

Support for ADT's and separately compiled modules.
Support for exception handling.
Automatic storage management via garbage collection.

ML currently being used to produce large systems. Language of choice in programming language research and implementation at CMU C.S. dept.

Computational biology: Human genome project at U. Penn. w/ Jon Crabtree '93

Lots of research into extensions. ML 2000 report. (Jon Riecke '86 on committee)
Addition of object-oriented features?

Major elements of programming languages:

Syntax, Semantics, Pragmatics

Syntax: Readable, writable, easy to translate, unambiguous, ...

Formal Grammars: Backus & Naur, Chomsky

First used in ALGOL 60 Report - formal description
Generative description of language.
Language is set of strings. (E.g. all legal ALGOL 60 programs)

Example

<expression>  ::= <term> | <expression> <addop> <term>
<term>        ::= <factor> | <term> <multop><factor>
<factor>      ::= <identifier> | <literal> | (<expression>)
<identifier>  ::= a | b | c | d
<literal>     ::= <digit> | <digit> <literal>
<digit>       ::= 0 | 1 | 2 | ... | 9
<addop>       ::= + | - | or
<multop>      ::= * | / | div | mod | and

Generates: a + b * c + b - parse tree

Grammar gives precedence and which direction op's associate

Extended BNF handy:

item enclosed in square brackets is optional

<conditional> ::= if <expression> then <statement> [else <statement>]

item enclosed in curly brackets means zero or more occurrences
```
<literal>::= <digit> { <digit> }
```

Syntax diagrams - alternative to BNF,
Syntax diagrams are never recursive, use "loops" instead.

Problems with Ambiguity

Suppose given grammar:

<statement>     ::= <unconditional> | <conditional>
<unconditional> ::= <assignment> | <for loop> | begin {<statement>} end
<conditional> ::= if <expression> then <statement> |
                  if <expression> then <statement> else <statement>

How do you parse : if exp1 then if exp2 then stat1 else stat2?

Could be

if exp1 then (if exp2 then stat1 else stat2) or
if exp1 then (if exp2 then stat1) else stat2

I.e. What happens if exp1 is true and exp2 is false?

Ambiguous

Pascal rule: else attached to nearest then

To get second form, write:

if exp1 then 
		begin 
			if exp2 then stat1 
		end 
	else 
		stat2

C has similar ambiguity.

MODULA-2 and ALGOL 68 require "end" to terminate conditional:

if exp1 then if exp2 then stat1 else stat2 end end
if exp1 then if exp2 then stat1 end else stat2 end

(Algol 68 actually uses fi instead of end)

Why isn't it a problem in ML?

Ambiguity in general is undecidable

Chomsky developed mathematical theory of programming languages:

type 0: recursively enumerable
type 1: context-sensitive
type 2: context-free
type 3: regular

BNF (or syntax diagrams) = context-free
can be recognized by push-down automata

Not all aspects of programming language syntax are context-free.

Declaration before use.
Go to

Formal description of syntax allows:

programmer to generate syntactically correct programs.
parser to recognize syntactically correct programs.

Parser-generators (also lexical analysis)- LEX, YACC (available in C and many other languages, e.g., ML), Cornell Program Synthesizer Generator.

Read carefully in text about parse trees and abstract syntax trees.

In reading, skim lightly over 4.6 & 4.7 to get main ideas.

Abstraction

Programming language creates a virtual machine for programmer.

Dijkstra: Originally we were obligated to write programs so that a computer could execute them. Now we write the programs and the computer has the obligation to understand and execute them.

Progress in programming language design marked by increasing support for abstraction.

Computer at lowest level is set of charged particles racing through wires w/ memory locations set to one and off - very hard to deal with.

In computer organization look at higher level of abstraction:
interpret sequences of on/off as data (reals, integers, char's, etc) and as instructions.

Computer looks at current instruction and contents of memory, then does something to another chunk of memory (incl. registers, accumulators, program counter, etc.)

When write Pascal (or other language) program - work with different virtual machine.