Assignment 2 Due 3/4/97

1. One of the advantages of functional languages is the ability to write high-level functions which capture general patterns. For instance, in class we defined the "listify" function which could be used to make a binary operation apply to an entire list.

   a. Your assignment is to write a high-level function to support list abstractions. The language Miranda allows the user to write list abstractions of the form:

           [f(x) | x <- startlist; cond(x)]
   

   where startlist is a list of type 'a, f : 'a -> 'b (for some type 'b), and cond : 'a -> bool. This expression results in a list containing all elements of the form f(x), where x is an element in the list, "startlist", and "cond(x)" is true. For example, if sqr(x) = x*x and odd(x) is true iff x is an odd integer, then

           [sqr(x) | x <- [1,2,5,4,3]; odd(x)]
   

   returns the list [1,25,9] (that is, the squares of the odd elements of the list - 1,5,3). Note that the list returned preserves the order of startlist.

   You are to write a function

           listcomp f startlist cond : ('a -> 'b) -> ('a list) -> 
                                                   ('a -> bool) -> ('b list)
   

   so that

           listcomp f startlist cond = 
                                           [f(x) | x <- startlist; cond(x)].  
   

   (Hint: One way to do this is to divide the function up into two pieces, the first of which calculates the list, [x | x <- startlist; cond(x)], and then think how the "map" function can be used to compute the final answer. It's also pretty straightforward to do it all at once.)

   b. Test your function by writing a function which extracts the list of all names of managerial employees over the age of 60 from a list of employee records, each of which has the following fields: "name" which is a string, "age" which is an integer, and "status" which has a value of managerial, clerical, or manual. (Be sure to define this function correctly. I'm always amazed at the number of people who miss this problem by carelessness!)

   c. Generalize your function in part a to

           listcomp2 g slist1 slist2 cond = 
                               [g x y | x <- list1; y <- list2; cond x y].
   

2. Write a program, balance, which determines if a string of various kinds of parentheses is balanced. Use a stack to check for matching parentheses (yes, I know it would be easy just using a general list or writing the whole routine recursively and not using any other data structure, but I want you to get some experience with user-defined types). Recall that the general idea is to push left parentheses on the stack and then pop them off when the corresponding right parenthesis is encountered.

   Use the definition:

               datatype 'a stack = Empty | Push of 'a * ('a stack )
   

   in your program. Be sure to write a pop routine for the stack. (Hint: It is trivial if you use pattern matching. Define pop Empty = Empty, or, if you are willing to learn about exceptions on your own, raise an exception.) Note that balance should have type string -> bool. Your program should treat "(", ")" and "[", "]" as parenthesis pairs. All other characters should be ignored. Thus, balance "(a*[b-(c/d)] -r)" should return true, while balance "(a*[b-(c/d]] -r)" should return false.

   (Hint: You may find it useful to use the built-in function, explode, which takes a string to a list of the characters in the list. E.g., explode "hello" = ["h","e","l","l","o"].)

3. In this problem, I want you to write an ML program which evaluates simple arithmetic expressions. Our expression language is very simple. It involves expressions written in the language given by the following simple BNF grammar.

           e ::= n | ~e | e + e | e - e | e * e | e / e | (e)
   

   In the above, "n" stands for an integer, "~e" is the negative of e, the next four terms are the sum, difference, product, and quotient of expressions, while (e) is used to determine the order of evaluation of expressions (e.g. 3 * (5 - 1)).

   Rather than working directly with the syntax above, we will presume that we have a parser which parses input into an abstract syntax tree, which your interpreter should use. Abstract syntax trees are just a convenient method of expressing parsed expressions; the definition of the ML datatype is

       datatype arithExp = 
                   AST_NUM of int | AST_NEG of arithExp | 
                   AST_PLUS of  (arithExp * arithExp) |
                   AST_MINUS of  (arithExp * arithExp) |
                   AST_PRODUCT of  (arithExp * arithExp) |
                   AST_QUOTIENT of  (arithExp * arithExp);
   

   Note how this definition mirrors the BNF grammar given above; for instance, the constructor AST_NUM makes an integer into an arithExp, and the constructor AST_PLUS makes a pair of arithExp's into an arithExp representing their sum. Interpreting abstract syntax trees is much easier than trying to interpret terms directly.

   Note that we no longer need the parentheses to group terms, as the example given above would simply be represented by:

           AST_PRODUCT (AST_NUM 3, AST_MINUS(AST_NUM 5,AST_NUM 1))
   

   which represents the parse tree which looks like:

   

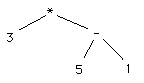
   You are to write an ML function evaluate that takes an abstract syntax tree representing an arithExp and returns the result of evaluating it. Most of the time when you evaluate the tree, you will get an integer, but if evaluating the expression results in a division by zero, it should return an error message. To allow both of these to be returned, we define

           datatype arithValue = NUM of int | ERROR;
   

   Thus you will define evaluate: arithExp -> arithValue, where as usual, the parse trees where the operation at the root is a binary operator are evaluated by evaluating the left and right subtrees and then performing the appropriate operation on the results. Evaluating AST_NUM expressions should be trivial, and AST_NEG's aren't much harder. Notice that if any subtree evaluates to ERROR, then the whole tree should evaluate to ERROR.

   To get you started, here is the beginning of the definition of evaluate:

           fun evaluate (AST_NUM n) = NUM n
             | evaluate ...