CSCI 256 Design and analysis of algorithms Solution to Assignment 7 Due Friday, 4/6/2001

Only turn in problems from the second section.

Practice problems:

1. Problem 17.2-4 on page 337 of the text. Professor Midas drives an automobile from Newark to Reno along Interstate 80. His car's gas tank, when full, holds enough gas to travel n miles, and his map gives the distances between gas stations on his route. The professor wishes to make as few gas stops as possible along the way. Give an efficient method by which Professor Midas can determine at which gas stations he should stop, and prove that your strategy yields an optimal solution.

   The strategy is quite simple. Make the first stop at the gas station as close to (but less than or equal) n miles from the start. Use a similar strategy for each successive stop. I.e., go as far as possible without running out of gas.

   We claim this is optimal. We prove this by showing that the greedy algorithm has no more stops than an optimal algorithm, O. Let the kth stop be the first that is not the same in the greedy and optimal algorithms. (If there are no differences, then clearly the optimal and greedy algorithms are equally good!) Because the k-1st stop was the same for both algorithms, the kth stop in both the greedy and the O algorithm are within n miles of the previous stop, but the greedy algorithm's stop must be a bit farther along. If we modify the O algorithm so that the kth stop is changed to that of the greedy algorithm, it is attainable, and it causes no harm, in that if the k+1st stop was accessible from O's kth stop, then it is certainly attainable from the greedy algorithms kth stop. Thus the modified O algorithm now matches the greedy algorithm at least through the kth stop. Since we can do this for all k, we can modify the O algorithm to match the greedy algorithm while retaining exactly the same number of stops. As a result, the greedy algorithm is also optimal.

2. Problem 17.3-2 on page 344 of the text. What is an optimal Huffman code for the following set of frequencies, based on the first 8 Fibonacci numbers?

       a:1  b:1  kc:2  d:3  e:5  f:8  g:13  h:21

   Solution:

       a = 0000000
       b = 0000001
       c = 000001
       d = 00001
       e = 0001
       f = 001
       g = 01
       h = 1

   We can generalize as follows. If we have n letters, such that a_k has frequency F_k for k = 0 to n-1, then the code for a₀ consists of n-1 0's. For 0 < i < n, the code for a_i consists of n-i-1 0's followed by a 1. This will always be the case because the sum of F_i < F₀ + ... + F_i-1 < F_i+1. Thus when building the trees for the Huffman codes, the current tree (built from characters a₀ through a_i-1 is always joined to the one node corresponding to a_i, as they are the trees with the lowest frequencies.

3. Problem 18.1-3 on page 360 of the text. A sequence of n operations is performed on a data structure. The ith operation costs i if i is an exact power of 2 and 1 otherwise. Use an aggregate method of analysis to determine the amortized cost per operation.

   Solution: The easiest way to count the operations is to count the total number of operations if n is a power of 2. We claim that if n = 2^k, then the total number of operations is 2^k+1 + 2^k - k - 2 = 3n - 2 (lg n) - 2.

   If k = 0, then n = 1, which costs 1 = 2¹ + 2⁰ - 0 - 2.
   Suppose the cost is as claimed for k. Show it for k+1. Let n = 2^k+1. To get this number of operations, perform the first n/2 = 2^k operations, which cost a total of 2^k+1 + 2^k - k - 2 by induction. Then n/2 - 1 = 2^k - 1 operations which cost 1 unit each (because none is a power of two), and then the nth operations, which costs n = 2^k+1. Thus the total cost is

       2k+1  + 2k - k - 2 + 2k - 1 + 2k+1 
           = 2*2k+1 + 2*2k - k -2 - 1 
           = 2k+2 + 2k+1 - (k+1) - 2

   as desired.

   If n is not a power of two, then let m be the greatest power of 2 less than or equal to n. The cost of the first n operations is the cost of the first m plus the remaining n-m. This gives 3m - 2 (lg m) - 2 + (n-m) < 4*n.

Problems to be turned in:

1. Optimal Merging: Let F₁, F₂, ..., F_n be files with lengths l₁, ..., l_n. We would like to merge all of the files together to make a single file, but we are only allowed to merge two at a time. For example if we had 3 files, we could merge the first two, and then merge the last with the new merged file. Alternatively we could have started by merging the last two or the first and third. The cost of merging two files is m+n if the files have length m and n. If the three files have lengths 10, 20, and 30, then the first merging the first two and then the third gives a total cost of 90 steps (30 for merging the first two and then another 60 for merging that new file with the third file), while merging the last two first gives a total cost of 110. In this problem I'd like you to develop an optimal greedy algorithm for merging collections of files. Hint: The development of this algorithm is almost identical to that of Huffman codes, so you should review that algorithm first.

   1. For each ordering of merges for files, we can define a binary merge tree. The leaves should represent the starting files, and should be labelled with the lengths of the files. The interior nodes should represent the result of merging the child nodes (and should be labelled with the cost of merging the children). For example, if files F₁ and F₂ are merged at one step of the algorithm, then the corresponding leaves should share the common parent node, N, which should be labelled with the sum of the lengths of those files. If you do this properly, the root should be labelled with the sum of the lengths of all of the files.

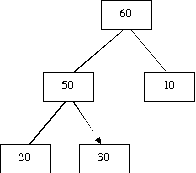
      For each of the orderings of merging the three files of lengths 10, 20, and 30, draw the corresponding binary merge tree.

      Solutions:

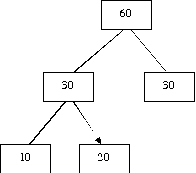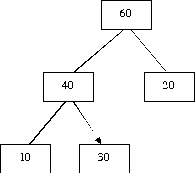   2. By examining the three trees computed in the previous part, create a formula computing the total cost of merging the files. This formula should involve the lengths of the files and the total depth of the leaf representing each file. Hint: Look at the trees and corresponding formulas for Huffman codes.

      Solution: Let d_i be the distance from the root to leaf corresponding to F_i, and let l_i be the length of F_i. Then the total cost of the merge tree is the sum for i = 1 to n of d_i * l_i.

   3. Describe a greedy algorithm for finding the optimal merge order for a collection of n files with lengths l₁, ..., l_n. You need not prove that the algorithm gives the optimal merge order (though it would be nice if you did understand why!).

      Solution: The solution is virtually identical to that for Huffman codes. Take the two shortest files and form a tree with those two as the roots. Replace those files in the collection by a new file whose length is the sum of the two originals. Continue this way, always merging the two shortest files until there is only one file left. The tree corresponds to the merge tree with lowest total cost. The proof that it is minimal cost is identical to the proof for Huffman codes.

2. Problem 18.2-2 on page 363 of the text. Redo exercise 18.1-3 (above) using an accounting method of analysis.

   Solution: Charge $3 for every operation. The idea is to leave $2 on every operation after the last power of 2. Show the balance is always non-negative. First operation costs $1, so $2 left on it. Next operation costs $2, so $1 left on it. For each operation after the last power of 2, charge $3, but cost is only $1. Therefore leave extra $2 on that operation. When come to operation n = 2^k, previous n/2-1 operations all have $2 left on them, plus have $3 for new operation. Therefore have $2*(n/2 -1) + $3 = $n+1 available to pay off cost of $n. Therefore amortized cost is less than or equal to $3 per operation.

Back to: