static boolean isPath(Graph g, Object startLabel, Object finishLabel)
{
Stack s = new StackList();
s.push(startLabel);
g.reset();
while (!s.isEmpty())
{
Object current = s.pop();
if (!g.isVisited(current))
{
g.visit(current);
if (current.equals(finishLabel))
return true;
for (Iterator nbrIterator = g.neighbors(vertexLabel);
nbrIterator.hasMoreElements();
nbrIterator.nextElement())
s.push(nbrIterator.value());
}
}
return false;
}
Complexity: Start by pushing and popping original vertex. Then for each unvisited node, push all neighbors on stack. Sum of degrees of all vertices = 2 * (# edges).
Thus complexity = O(e), if e is number of edges. (Note some vertices may never get reached, so don't have to add O(v). If also cycle through all vertices then O(v+e).)
Again easy to modify to mark all reachable vertices.
What order does this do search in?
What would happen if we used a queue instead of a stack?
Breadth-First visits as few vertices as possible before 'backtracking' (removing a vertex from the queue). Thus neighbors of V are visited first, then neighbors of neighbors, etc.
Priority-First Traversal (Priority Queue Based)
Vertices to be visited next are put on a priority queue
What if we wanted to classify all vertices in terms of which component they are in?
------------------------
Algorithm called Dijkstra's algorithm finds shortest path from one node to another. Uses a "greedy" style algorithm which keeps adding vertices which are closest to start. Uses a priority queue to establish which item to consider next.
Suppose we have a directed graph with no cycles (acyclic). Directed acyclic graph is sometimes called a DAG.
We would like to list all elements in an order which is consistent with the graph ordering. I.e., so all edges point same direction.
Can be helpful if need to perform tasks in some order and some tasks can only be accomplished after some others are done

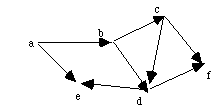
The idea of sorting algorithm is that if we do a depth-first search, then complete a node only when all nodes reachable from it have been completed:
Do a, b, c, f, $f, d, e, $e, $d, $c, $b, $a where $ means backing up from node.
Sorted order is: a, b, c, d, e, f
Thus when return from node, add it to front of list. Then have sorted list when done:
For variety, write it in a subclass of one of graphs:
class TopoSortGraph extends DirectedMatrixGraph
{
public void topSort()
{
List orderList = new SinglyLinkedList();
Iterator vertexIt = elements();
for (vertexIt .reset(); vertexIt.hasMoreElements(); vertexIt.nextElement())
{
if (isVisited(vertexIt .value())
DFS(vi.value(),orderList);
}
return orderList;
}
public void DFS(Object node, List orderList)
{
visit(node);
Iterator nbrIt = neighbors(node);
for (nbrIt.reset(); nbrIt.hasMoreElements; nbrIt.nextElement())
{
if (!isVisited(nbrIt.value()))
DFS(nbrIt.value(),orderList);
}
orderList.add(node)
}
Differs from algorithm in text in that return in order so arrows go left to right (text's version went from right to left) and wrote it as subclass of GraphMatrixDirected.
(Note can write in exactly same way so as to be subclass of GraphListDirected.)
If graph really were a tree, what order would elements end up in list?
public interface Dictionary extends Container
{
public Object put(Object key, Object value);
// pre: key is non-null
// post: puts key-value pair in Dictionary,
// returns old value
public boolean contains(Object value);
// pre: value is non-null
// post: returns true iff the dictionary contains the value
public boolean containsKey(Object key);
// pre: key is non-null
// post: returns true iff the dictionary contains the key
public Object remove(Object key);
// pre: value is non-null
// post: removes an object "equal" to value within bag.
public Object get(Object key);
// pre: key is non-null
// post: returns value associated with key, in table
public Iterator keys();
// post: returns iterator for traversing keys in dictionary
public Iterator elements();
// post: returns iterator for traversing values in
// dictionary
public int size();
// post: returns number of elements in dictionary
}
| Structure | Search | Insert | Delete | Space |
|---|---|---|---|---|
| Linked List | O(n) | O(1) | O(n) | O(n) |
| Sorted Array | O(log n) | O(n) | O(n) | O(N) |
| Balanced BST | O(log n) | O(log n) | O(log n) | O(n) |
| Array[KeyRange] of EltType | O(1) | O(1) | O(1) | KeyRange |
Other possibilities include unordered array, ordered linked list, unbalanced BST.
We can get slightly more efficient algorithms with Sorted Arrays if we use an interpolation search (as long as know the distribution of keys). But it is still O(log n).
This implementation assumes that the data has a key which is of a restricted type (some enumerated type in Pascal, integers in Java), which is not always the case.
Note also that the size requirements for this implementation could be prohibitive.
Ex. If the array held 2000 student records indexed by social security number it would be declared as ARRAY[0..999,999,999]
What if most of entries are empty? If we use a smaller array then all elements will still fit.
Suppose we have a lot of data elements of type EltType and a set of locations in which we could store data elements.
Consider a function H: EltType -> Location with the properties
Instead we use something that behaves well, but not necessarily perfectly.
The goal is to scatter elements through the array randomly so that they won't bump into each other.
Define a function H: Keys -> Addresses, and call H(element.key) the home address of element.
Of course now we can't list elements easily in any kind of order, but hopefully we can find them in time O(1).
Note that each entry in the table will need to include the actual key, since several different keys will likely get mapped to the same subscript.
There are two problems to look at:
Here are some sample Hashing functions.
Presume for the moment that the keys are numbers.
Unfortunately it is easy to get a biased sample. We can carefully analyze keys to see which will work best. We must watch out for patterns - they should generate all possible table positions. (For example the first digits of SS#'s reflect the region in which they were assigned and hence usually would work poorly as a hashing function.)
This is very efficient and often gives good results if the TableSize is chosen properly.
If it is chosen poorly then you can get very poor results. If TableSize = 28 = 256 and the keys are integer ASCII equivalent of two letter pairs, i.e. Key(xy) = 28 * ORD(x) + ORD(y), then all pairs starting ending with the same letter get mapped to same address. Similar problems arise with any power of 2.
The best bet seems to be to let the TableSize be a prime number.
In practice if no divisor of the TableSize is less than 20, the hash function seems to be OK. (Text uses 997 in the sample program)
Example: Let the keys range between 1 and 32000 and let the TableSize be 2048 = 211.
Square the Key and remove the middle 11 bits. (Grabbing certain bits of a word is easy to do using shift operators in assembly language or can be done using the div and mod operators using powers of two.)
In general r bits gives a table of size 2r.
This is often used if the key is too big. E.g., If the keys are Social security numbers, the 9 digits will generally not fit into an integer. Break it up into three pieces - the 1st digit, the next 4, and then the last 4. Then add them together.
Now you can do arithmetic on them.
This technique is often used in conjunction with other methods (e.g. division)
If you use longints to hold the numbers, then you can get 4 letters into one number in this way. If they are all alphabetic (no special characters), then you can subtract (int)'a' from each ASCII code in order to reduce the size of the keys.
Here is a very simple-minded hash code for strings: Add together the ordinal equivalent of all letters and take the remainder mod tableSize.
Problem: Words with same letters get mapped to same places:
miles, slime, smile
This would be much improved if you took the letters in pairs before division.
Nevertheless, for simplicity we adopt this simple-minded (and thus relatively useless) hash function for the following discussion.
Here is a function which adds up ord of letters and then mod tableSize:
hash = 0;
for (int charNo = 0; charNo < word.length(); charNo++)
hash = hash + (int)(word.charAt(CharNo));
hash = hash % tableSize; (* gives 0 <= hash < tableSize *)
Code is only a little more complex to multiply each succeeding character by 2*8.
Efficient way using Horner's rule:
hash = 0;
for (in CharNo = word.length()-1;charNo >= 0; charNo--)
hash = (256*hash + (int)(word.charAt(CharNo))) % tableSize;
Notice we mod by tableSize each time we update hash to prevent overflows.
Efficient way of calculating uses only word.length() multiplications, while normal way would involve O(word.length()2) multiplications.