Recall that insertion, search, and deletion in a balanced tree have time complexity O(h), where h is the height of the tree. In the best case this can be O(log n), but in the worst, O(n). We will investigate ways of maintaining balance in trees using rotations that cost at most O(log n) then all of these operations can be done in time O(log n).
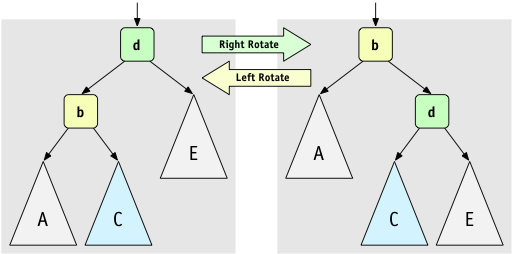
Our basic operations will involve rotating trees to bring them back into balance. The two fundamental operations are the following:

These operations will be used in building AVL or Red-Black trees.
An AVL tree is a binary search tree which has the following properties:
Note that this does not guarantee that a tree is balanced (i.e., of minimum height). For example, the following is AVL:
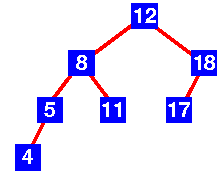
E,
increasing its height by one.
 The tree is now unbalanced; how would we rebalance it?
Performing a left rotation fixes the problem.
The tree is now unbalanced; how would we rebalance it?
Performing a left rotation fixes the problem.
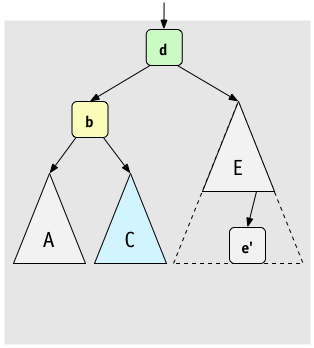 Note that we started with an unbalanced node, d, where its right subtree is
bigger by 2, and it was itself a right subtree
Note that we started with an unbalanced node, d, where its right subtree is
bigger by 2, and it was itself a right subtree
D,
increasing its height by one.
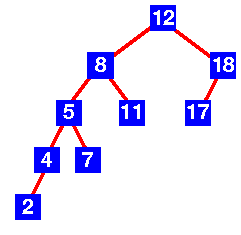
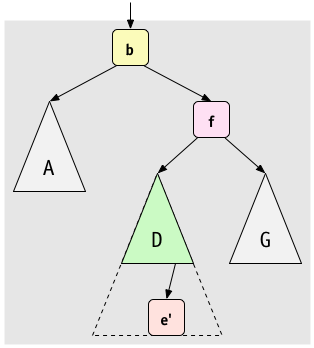 The tree is now unbalanced; how would we rebalance it?
Performing a left rotation does not help!
The tree is now unbalanced; how would we rebalance it?
Performing a left rotation does not help!
 No single rotation will help. We'll have to do a double rotation.
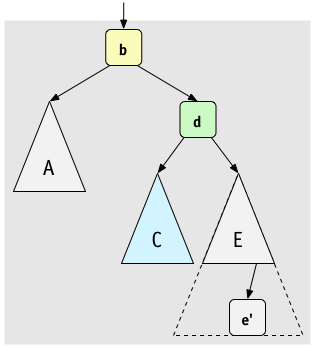
We'll assume that the new node is in subtree
No single rotation will help. We'll have to do a double rotation.
We'll assume that the new node is in subtree E (you could also
draw it under C too, as we'll see).
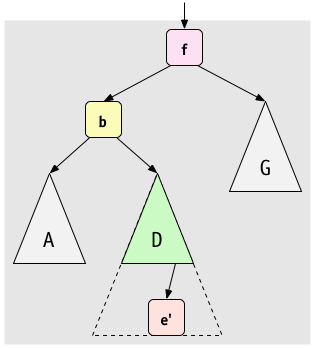
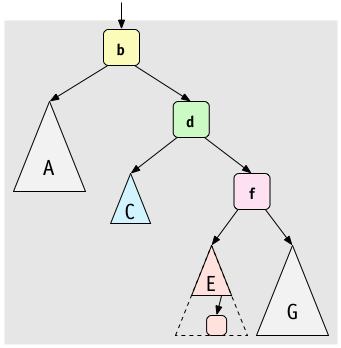
 To rebalance the tree
Rotate right at
To rebalance the tree
Rotate right at f
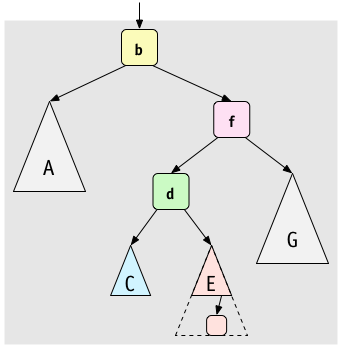
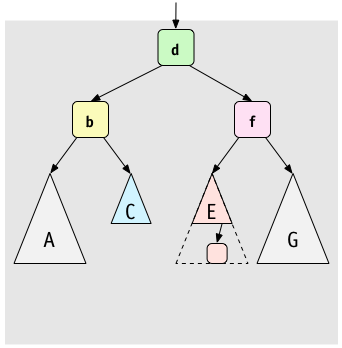
 Then, rotate left at
Then, rotate left at b
 Pictures thanks to Melissa O'Neill
Pictures thanks to Melissa O'Neill
The text refers to these operations as trinode restructurings. The insert and remove operations proceed as before, but then we walk up the tree from the inserted (or removed) node to the root, restructuring when we come to an unbalanced node. There are lots of different cases, but all can be solved by using either one or two rotations as you move farther up toward the node. (Note that if you ever modify a node to be completely balanced, then get to stop as no added imbalances)
We can accomplish this in Java by keeping an extra field at each node that records the balance factor, which is the difference between the heights of its left and right subtrees. Note that the allowable values are -1, 0, and +1 for an AVL tree. When a node is added, we walk up the tree to the root, recalculating the balance factors for each node on the path. If it ever becomes unbalanced (i.e., the absolute value of the balance factor exceeds 1), then rotations are invoked to rebalance the node.
Removal works similarly, but start from node removed at the bottom of the tree.
You can take a look at how insertion and removal works in AVL trees in the following AVL applet. I recommend that you click on "thought control" in the middle of the left edge of the applet.
We will skip splay trees, but look quickly at red-black trees.Red-black trees also maintain balance, but restructuring only O(1) after an update.
A red-black tree is a binary search tree with nodes colored red and black in a way that satisfies the following properties:
Proposition: The height of a red-black tree storing n entries is O(log n). In fact, log(n+1) <= h <= 2 log(n+1).
The idea behind this is if we erase the red nodes then the tree will be perfectly balanced. Hence the black height = log (# black nodes). The red nodes can at most double the length of a path.